Déborah Boyenval

About Me

I’m currently a postdoctoral fellow at LaBRI in the MTV team with Loïc Paulevé. I’m also working with the BRIC’s sc-RNA Seq data on the application of formal methods developed within the BNeDiction project to explain the phenotype of uncoupling of Hematopoietic Stem Cells (HSCs) from hematopoiesis in aged mice, a phenotype related to a decline in the development of the lymphoid lineage and immunodeficiency.

During my Ph.D, I worked in the field of formal modeling of biological systems, also called symbolic systems biology by the GT-Bioss. Monthly seminars are organized so feel free to take a look if you’re new to the field! My PhD thesis focuses on the discrete modeling of intrinsic cell cycle checkpoints and was supervised by Gilles Bernot, Jean-Paul Comet and Franck Delaunay. I was part of two research teams: the SPARKS team in I3S lab (Sophia Antipolis, France) specialized in formal methods applied to systems biology, and Franck Delaunay’s team in iBV (Nice, France) devoted to the experimental study of interactions between mammalian peripheral circadian clocks, the cell cycle and metabolism under healthy and pathological conditions.

Research Interests

• Discrete modeling of complex biological phenomena: formal specification of biological checkpoints in regulatory biological systems, coupling between circadian cycle, cell cycle and metabolism, the link between aging and an altered hematopoiesis.
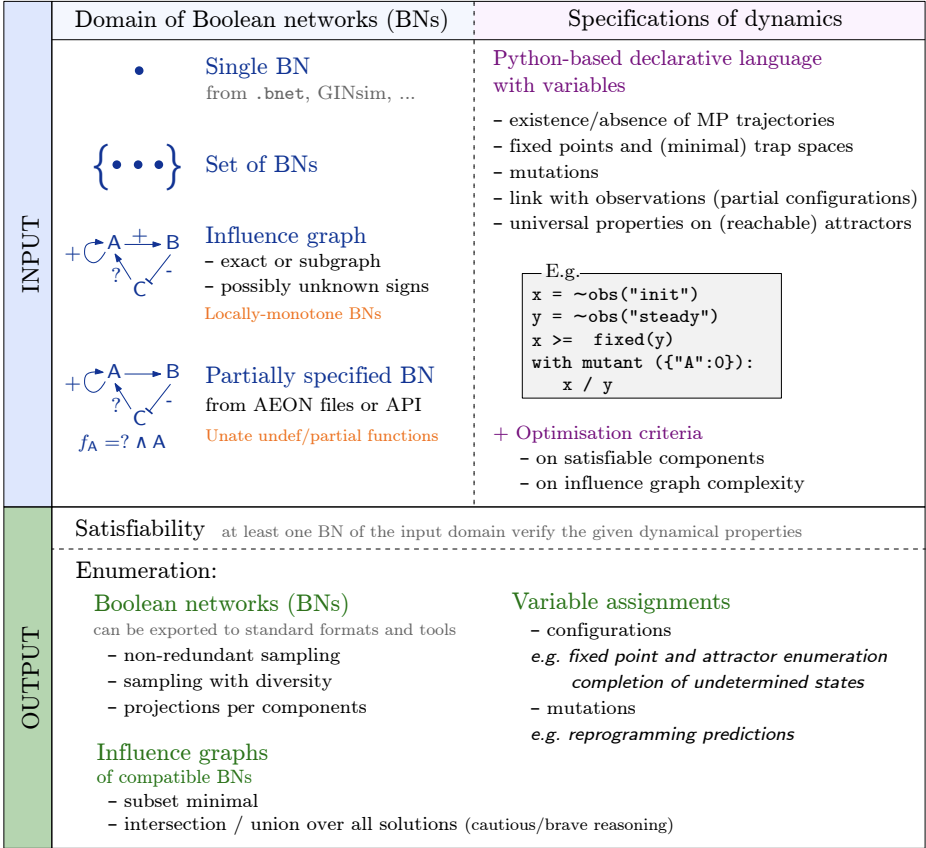
• Formal methods applied to system biology: model-checking, (genetically-modified) Hoare’s logic, automatic parameter identification of a parameterized interaction graph (Thomas’ formalism), ASP, synthesis and reprogramming of boolean networks (more in the application so far)
• Integration of omics data for modeling of discrete biological systems: RNA velocity analysis, trajectory inference, identification of cellular type boolean signature.

More about my Ph.D thesis

My Ph.D thesis was initially motivated by a need to model the coupling between the circadian cycle, the cell cycle and metabolism, with the prospect of (better) understanding the circadian chrono-toxicity and efficacy of anti-cancer drugs. During my first year as Ph.D student, I repositioned the problem on the question of the dynamic specifications of such a coupling. What are the dynamic characteristics of the coupling itself, apart from the union of the dynamic characteristics of the three modules?

I propose a focus on the notion of biological checkpoint, which is described very intuitively as a set of steps that must be completed before starting another. This discrete notion applies reasonably well in the case of cell cycle regulation, since it is described dynamically by a set of switch-like molecular events of activation and inhibition of the cell cycle core regulators. A checkpoint is thought here as a constraint on the order of some blocks of cell cycle events named phases. Here we refer to the phases :

• S: DNA replication,
• M: Fair distribution and division of DNA
• G1 (prior S) and G2 (prior M): gap phases for energy and biomass resources.

DNA replication and division are highly regulated processes. Errors in DNA copying or distribution in descendant cells must be limited for the survival of the species. A widely cited example cell fusion experiments show that certain phases cannot occur simultaneously and that there is an order of phases to preserve DNA integrity (great scheme here). A G2 cell, ready to enter M phase, is merged with an S phase cell. The G2 cell halts its progression and does not enter M phase. In addition, the G2 cell does not start a new DNA synthesis phase. This G2 cell appears to be temporally isolated from the S and M phase. This remarkable experiment shows that :

• The G2 –> S transition seems to be possible only when a new cell cycle begins, i.e. only after the M phase, so the transition S/G2 is irreversible (unidirectionality).
• The G2 –> M transition is only possible when the S phase has ended, this is an example of phase order constraint.

If we reason in terms of transition system, two phases x and y (in blue) are temporally isolated if it is not possible to reach y from x by any path without passing through a transition state that certifies that phase x has ended (in green). Furthermore, there is no way to reach x from y without passing through a state of y that certifies that y is a completed phase (in green).

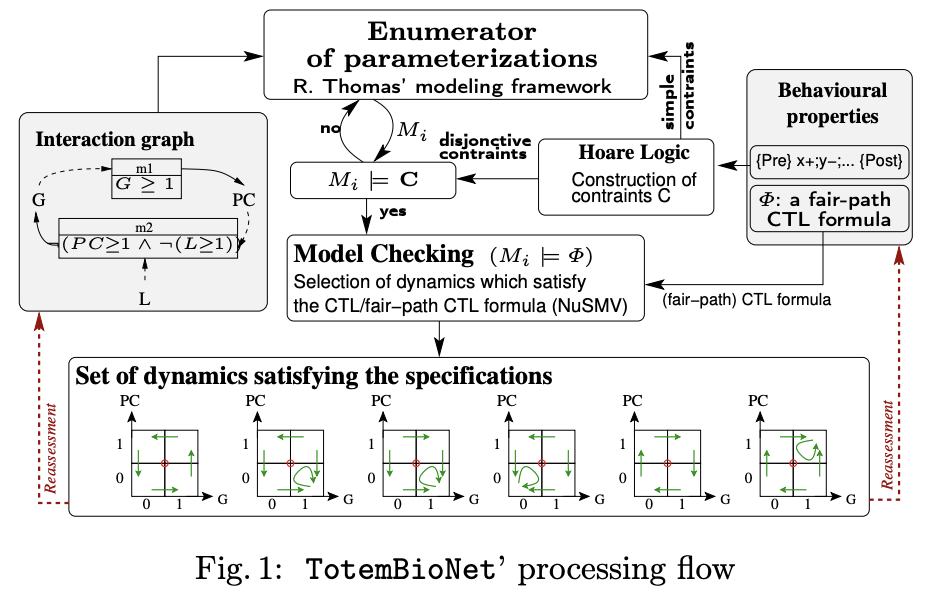
Discrete formalisms for modeling biological regulatory networks, such as boolean/multivaluated networks or Thomas’ formalism, are well suited to the study of temporal phase separation, described by these forbidden paths between phases. Thomas’ formalism has been coupled with formal methods for selecting discrete models, such as model-checking or Hoare’s logic. The idea was simple: only those models are selected which satisfy the interaction graph given as input, as well as dynamic specifications on observed biological traces (Hoare logic) or broader dynamic specifications such as CTL. The interaction graph of mammalian cell cycle progression used for the proof-of-concept was entirely renovated from Jonathan Behaegel’s seminal model, itself an update and discretization of Tyson and Novak’s model. I have abstracted each phase of the cell cycle by a set of activation or inhibition events of the cell cycle regulators from the rich literature available on the subject. Based on these phases specification that have been formally proven correct using Hoare logic, it was then possible to reason about the notion of temporal separation with model-checking of CTL formulas. Thanks to all these materials, my Ph.D team and I were able to model the checkpoints G1/S, S/G2, G2/M and the metaphase/anaphase transition checkpoint, thus proving that a checkpoint is a discrete, non-continuous, concept.

Would you like to find out more? Go to the Publications tab below.

A checkpoint in the broadest sense constrains any type of event. I took the example of the cell cycle in my thesis since the problem focuses on a single physiological system which turns out to be the most documented example of checkpoint-regulated system in biology. Complicating the issue, metabolism is intrinsically involved in the progression of the cell cycle. The circadian system coordinates physiological processes over 24 hours. Apart from the chronometric aspect, my thesis poses an open question: does the circadian system act as a checkpoint (i.e. a temporal separator) between the phases of the cell cycle (G1, S, G2, M) and metabolism (oxydative, reductive)?

More About My (First) Postdoc

Under construction, I still need to step back.

News

• [June. 2024] Our paper about BoNesis tool is accepted to CMSB 2024.

• [June. 2024] I received the Prix de thèse de la Fondation Université Côte d’Azur (Ph.D thesis award).

Publications

Talks and posters

• [Talk, December 2023] Formal modeling of the discrete dynamics of intrinsic cell cycle checkpoints: a proof of concept at GT-Bioss.
• [Ph.D Defense, December 2022] Formal modeling of biological cyclic behavior with checkpoints: the cell cycle regulation at I3S laboratory.
  (Slides).
• [Talk, March 2022] A discrete modeling study devoted to the formalization and verification of mammalian cell cycle checkpoints at Lifeware Public Seminar.
  (Slides).
• [Talk, November 2021] Mammalian cell cycle, formalizing phases at GT-Bioss Annual Days.
  (Slides).
• [Poster, July 2021] Logical and incremental formalization of cell cycle checkpoints at JOBIM 2021.
  (Poster).
• [Talk, June 2021] Logical modeling in biology through the case study of the cell cycle and its checkpoints at a public seminar of the Institute of Biology of Valrose.
  (Slides).
• [Talk, November 2020] Study of cell cycle checkpoints, specification and verification at GT-Bioss mensual seminars.
  (Slides).
• [Talk, September 2020] What is a cell cycle checkpoint, The TotemBioNet answer at CMSB 2020.
  (Slides).
• [Talk, December 2019] From phase characterization toward observable properties verification, at NeuroMod Institute for a Public PhD Seminar (Sophia Antipolis, France).
  (Slides).
• [Poster, November 2019] Introduction of Priorities in Biological Regulatory Networks “à la Thomas” at Modelife Annual Meeting (Frejus, France).
  (Poster).
• [Poster, June. 2019] A discrete cell cycle model: from phase characterization toward observable properties verification, at a CNRS summer school about formal modeling of biological regulatory networks.
  (Poster).

Services

Teaching

I taught some computer science courses for 3 years during my Ph.D from September 2018 to June 2021 at the Université Côte d’Azur as well as at the engineering school Polytech’ Nice Sophia Antipolis.

• Systems and network administration (PeiP 1st year)
• Databases theory and its application in SQL (GB 4th year, B.sc. 2nd year)
• Introduction to the web (PeiP 2nd year)
• Web applications (PeiP 2nd year)
• Algorithmics (GB 4th year)
• Imperative programming with Python (GB 3rd year, B.sc. 1st year)

Science outreach

• [September 2022] A conference for Woman In Machine Learning (WiML) on the principle of model checking and a practical application in biology. You can find the slides here.

Graduate school

• [2020 - 2022] Treasurer of the DS4H graduate school student association
• [2021 - 2022] Elected student member of the DS4H graduate school scientific and pedagogical council.

Links

• Gilles Bernot (my former Ph.D supervisor) and the youtube channel “Qu’est-ce que tu GEEKes?” made a superb video about Gilles’ job as a university professor. His witty stories and remarks accompanied and nourished me throughout my thesis. Go this way.
• I’d like to share the websites of people I’ve met and who have inspired me over the years in my research : Cyrille Mascart, Julien Martinelli, Athénaïs Vaginay and Stéphanie Chevalier. I also recommend the website of Chloé-Agathe Azencott, which is full of resources for machine learning newbies.

Powered by Jekyll and Minimal Light theme.